- Tham gia
- 28/1/21
- Bài viết
- 86,154
- Điểm
- 113
tác giả
Bài tập tam giác đồng dạng có đáp án TUYỂN TẬP bài tập tam giác đồng dạng cạnh góc cạnh, CẠNH CẠNH CẠNH RẤT HAY
YOPOVN xin giới thiệu tài tập tam giác đồng dạng hình học lớp 8 có lời giải chi tiết. Bài tập tam giác đồng dạng có đáp án TUYỂN TẬP bài tập tam giác đồng dạng cạnh góc cạnh, CẠNH CẠNH CẠNH RẤT HAY. bao gồm 20 bài tập và được viết dưới dạng file word gồm 16 trang. Các bạn xem và tải về ở dưới.
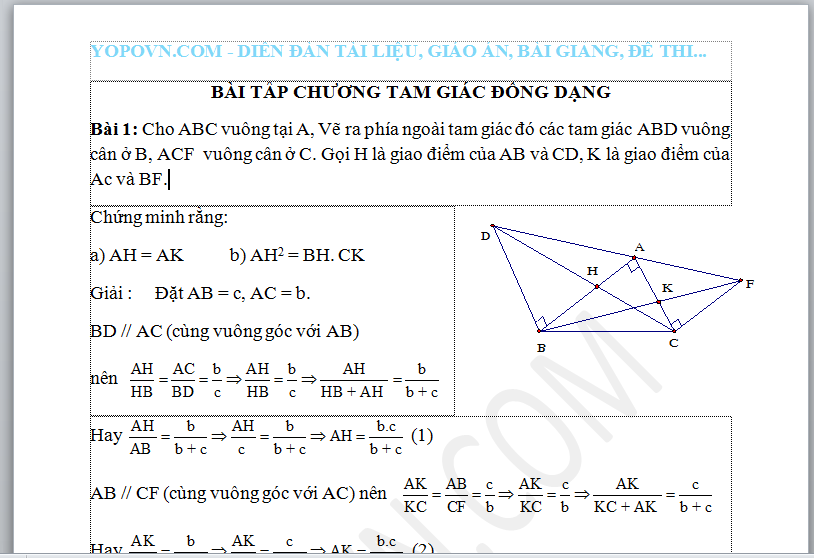
Bài 1: Cho ABC vuông tại A, Vẽ ra phía ngoài tam giác đó các tam giác ABD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và CD, K là giao điểm của Ac và BF.
Chứng minh rằng:
a) AH = AK b) AH2 = BH. CK
Giải : Đặt AB = c, AC = b.
BD // AC (cùng vuông góc với AB)
nên
Hay (1)
AB // CF (cùng vuông góc với AC) nên
Hay (2)
Từ (1) và (2) suy ra: AH = AK
b) Từ và suy ra (Vì AH = AK)
AH2 = BH . KC
Bài 2: Cho hình bình hành ABCD, đường thẳng a đi qua A lần lượt cắt BD, BC, DC theo thứ tự tại E, K, G. Chứng minh rằng:
a) AE2 = EK. EG b)
c) Khi đường thẳng a thay đổi vị trí nhưng vẫn qua A thì tích BK. DG có giá trị không đổi
Giải
a) Vì ABCD là hình bình hành và K BC nên
AD // BK, theo hệ quả của định lí Ta-lét ta có:
b) Ta có: ; nên
YOPOVN xin giới thiệu tài tập tam giác đồng dạng hình học lớp 8 có lời giải chi tiết. Bài tập tam giác đồng dạng có đáp án TUYỂN TẬP bài tập tam giác đồng dạng cạnh góc cạnh, CẠNH CẠNH CẠNH RẤT HAY. bao gồm 20 bài tập và được viết dưới dạng file word gồm 16 trang. Các bạn xem và tải về ở dưới.
BÀI TÂP CHƯƠNG TAM GIÁC ĐỒNG DẠNG
Bài 1: Cho ABC vuông tại A, Vẽ ra phía ngoài tam giác đó các tam giác ABD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và CD, K là giao điểm của Ac và BF.
Chứng minh rằng:
a) AH = AK b) AH2 = BH. CK
Giải : Đặt AB = c, AC = b.
BD // AC (cùng vuông góc với AB)
nên
Hay (1)
AB // CF (cùng vuông góc với AC) nên
Hay (2)
Từ (1) và (2) suy ra: AH = AK
b) Từ và suy ra (Vì AH = AK)
AH2 = BH . KC
Bài 2: Cho hình bình hành ABCD, đường thẳng a đi qua A lần lượt cắt BD, BC, DC theo thứ tự tại E, K, G. Chứng minh rằng:
a) AE2 = EK. EG b)
c) Khi đường thẳng a thay đổi vị trí nhưng vẫn qua A thì tích BK. DG có giá trị không đổi
Giải
a) Vì ABCD là hình bình hành và K BC nên
AD // BK, theo hệ quả của định lí Ta-lét ta có:
b) Ta có: ; nên





