- Tham gia
- 28/1/21
- Bài viết
- 86,007
- Điểm
- 113
tác giả
Tài liệu bồi dưỡng học sinh giỏi tin 11 TUYỂN TẬP tài liệu ôn thi học sinh giỏi tin học 11 RẤT HAY
Tài liệu bồi dưỡng HSG môn Tin 11, tài liệu bồi dưỡng hsg tin học thpt, tài liệu ôn thi học sinh giỏi tin học 11 được soạn dưới dạng file word và PDF gồm 290 trang. Các bạn xem và tải về ở dưới.
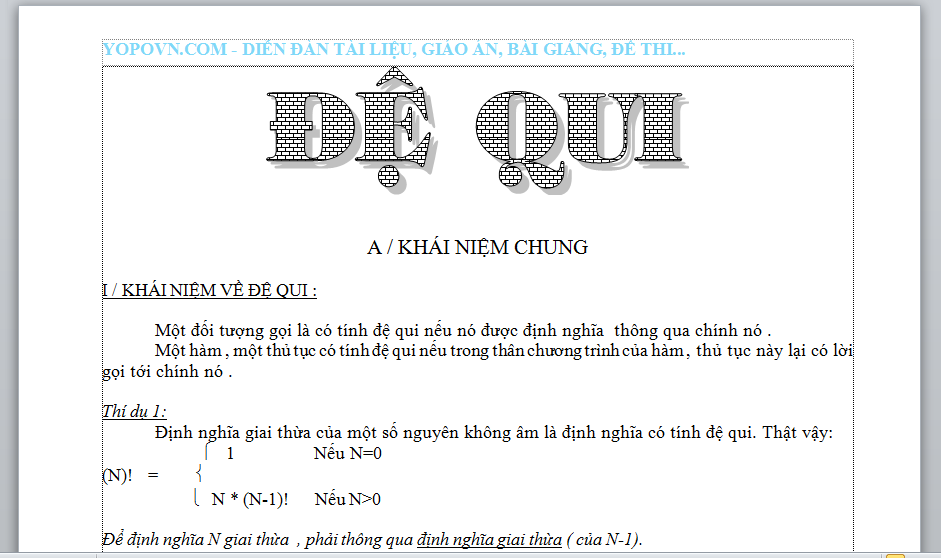
A / KHÁI NIỆM CHUNG
I / KHÁI NIỆM VỀ ĐỆ QUI :
Một đối tượng gọi là có tính đệ qui nếu nó được định nghĩa thông qua chính nó .
Một hàm , một thủ tục có tính đệ qui nếu trong thân chương trình của hàm , thủ tục này lại có lời gọi tới chính nó .
Thí dụ 1:
Định nghĩa giai thừa của một số nguyên không âm là định nghĩa có tính đệ qui. Thật vậy:
ì 1 Nếu N=0
(N)! = í
î N * (N-1)! Nếu N>0
Để định nghĩa N giai thừa , phải thông qua định nghĩa giai thừa ( của N-1).
Thí dụ 2:
Xây dựng hoán vị của N phần tử cũng có tính chất đệ qui . Thật vậy :
Giả sử có 1 hoán vị là S (A1 ,A 2 , ... A i-1 ,Ai ,..... An-1 ,An ), sau đó đổi chỗ 2 phần tử S và S[j] của hoán vị đó ta sẽ được một hoán vị mới .Sau đây là sơ đồ hình thành dần các hoán vị tiếp theo nhau của hoán vị S(1,2,3)
123
B1 : i =1 123 213 312
j = 1,2,3
B2 : i = 2 123 132 213 231 312 321 j=2,3
B3 : i =3 123 132 213 231 312 321
j=3
Vậy để xây dựng các hoán vị sau ta phải dựa vào các hoán vị đã sinh ra trước đó.
Thí dụ 3: Xây dựng tổ hợp chập K của N phần tử 1,2,3,...,N cũng theo phương thức đệ qui :
Ta sẽ xây dựng dần từng phần tử từ vị trí thứ 1 đến vị trí thứ K của tổ hợp .Để xây dựng phần tử thứ i ( sau khi đã xây dựng xong các phần tử từ 1 đến i-1 của tổ hợp này ) , ta sẽ cho phần tử thứ i nhận 1 trong các giá trị từ (Ai-1 +1) đến giá trị cao nhất có thể được của nó đó là giá trị (N-K)+i vì sau phần tử thứ i này còn (K-i) phần tử ,do đó nếu phần tử thứ i nhận giá trị cao nhất là (N-K)+i thì các phần tử tiếp theo vẫn còn khả năng nhận các giá trị : (N-K)+i +1 , (N-K)+i +2 , ...., (N-K)+i + (K-i) = N .
Vậy để xây dựng phần tử thứ i của 1 tổ hợp , ta phải dựa vào kết quả đã xây dựng tới phần tử thứ i-1 . Tất nhiên để xây dựng phần tử thứ 1 , ta phải dựa vào ‘phần tử hàng rào ‘ là phần tử ở vị trí thứ ‘0’ ,ta gán cho phần tử này giá trị nào cho phù hợp qui luật nêu trên ? rõ ràng đó là giá trị 0 ,nhằm cho nó quyền được bình đẳng như mọi phần tử khác .Phần tử 0 này chịu một trách nhiệm rất nặng nề ,bắt đầu từ nó mới xây dựng dần được các phần tử tiếp theo của mọi tổ hợp , song ta cũng đừng quên nó phải ‘ngậm ngùi’ vì ‘không được đứng trong tổ hợp ‘ .
XEM THÊM:
Tài liệu bồi dưỡng HSG môn Tin 11, tài liệu bồi dưỡng hsg tin học thpt, tài liệu ôn thi học sinh giỏi tin học 11 được soạn dưới dạng file word và PDF gồm 290 trang. Các bạn xem và tải về ở dưới.
A / KHÁI NIỆM CHUNG
I / KHÁI NIỆM VỀ ĐỆ QUI :
Một đối tượng gọi là có tính đệ qui nếu nó được định nghĩa thông qua chính nó .
Một hàm , một thủ tục có tính đệ qui nếu trong thân chương trình của hàm , thủ tục này lại có lời gọi tới chính nó .
Thí dụ 1:
Định nghĩa giai thừa của một số nguyên không âm là định nghĩa có tính đệ qui. Thật vậy:
ì 1 Nếu N=0
(N)! = í
î N * (N-1)! Nếu N>0
Để định nghĩa N giai thừa , phải thông qua định nghĩa giai thừa ( của N-1).
Thí dụ 2:
Xây dựng hoán vị của N phần tử cũng có tính chất đệ qui . Thật vậy :
Giả sử có 1 hoán vị là S (A1 ,A 2 , ... A i-1 ,Ai ,..... An-1 ,An ), sau đó đổi chỗ 2 phần tử S và S[j] của hoán vị đó ta sẽ được một hoán vị mới .Sau đây là sơ đồ hình thành dần các hoán vị tiếp theo nhau của hoán vị S(1,2,3)
123
B1 : i =1 123 213 312
j = 1,2,3
| |||
| |||
B2 : i = 2 123 132 213 231 312 321 j=2,3
| |||||||
| | | |||||
B3 : i =3 123 132 213 231 312 321
j=3
Vậy để xây dựng các hoán vị sau ta phải dựa vào các hoán vị đã sinh ra trước đó.
Thí dụ 3: Xây dựng tổ hợp chập K của N phần tử 1,2,3,...,N cũng theo phương thức đệ qui :
Ta sẽ xây dựng dần từng phần tử từ vị trí thứ 1 đến vị trí thứ K của tổ hợp .Để xây dựng phần tử thứ i ( sau khi đã xây dựng xong các phần tử từ 1 đến i-1 của tổ hợp này ) , ta sẽ cho phần tử thứ i nhận 1 trong các giá trị từ (Ai-1 +1) đến giá trị cao nhất có thể được của nó đó là giá trị (N-K)+i vì sau phần tử thứ i này còn (K-i) phần tử ,do đó nếu phần tử thứ i nhận giá trị cao nhất là (N-K)+i thì các phần tử tiếp theo vẫn còn khả năng nhận các giá trị : (N-K)+i +1 , (N-K)+i +2 , ...., (N-K)+i + (K-i) = N .
Vậy để xây dựng phần tử thứ i của 1 tổ hợp , ta phải dựa vào kết quả đã xây dựng tới phần tử thứ i-1 . Tất nhiên để xây dựng phần tử thứ 1 , ta phải dựa vào ‘phần tử hàng rào ‘ là phần tử ở vị trí thứ ‘0’ ,ta gán cho phần tử này giá trị nào cho phù hợp qui luật nêu trên ? rõ ràng đó là giá trị 0 ,nhằm cho nó quyền được bình đẳng như mọi phần tử khác .Phần tử 0 này chịu một trách nhiệm rất nặng nề ,bắt đầu từ nó mới xây dựng dần được các phần tử tiếp theo của mọi tổ hợp , song ta cũng đừng quên nó phải ‘ngậm ngùi’ vì ‘không được đứng trong tổ hợp ‘ .
XEM THÊM:




