- Tham gia
- 28/1/21
- Bài viết
- 86,029
- Điểm
- 113
tác giả
Tài liệu ôn thi vào lớp 10 môn toán violet NĂM 2022 - 2023
Trong bài viết này xin giới thiệu TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN. TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN giúp các em ôn luyện và thi môn Toán đạt kết quả cao, đồng thời đề thi cũng là tài liệu tốt giúp các thầy cô tham khảo trong quá trình dạy TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN.
PHẦN I: CÁC VẤN ĐỀ CƠ BẢN CỦA TOÁN 9
VẤN ĐỀ I: RÚT GỌN BIỂU THỨC CHỨA CĂN BẬC HAI
– Với hai số a và b không âm ta có:
+ nếu A < 0
+ Đặc biệt với A 0 ta có
+ Nếu A 0 và B 0 thì
+ Nếu A < 0 và B 0 thì
+ Nếu A 0 và B 0 thì
+ Nếu A < 0 và B 0 thì
– Với các biểu thức A, B mà A.B 0 và B 0, ta có
– Với các biểu thức A, B mà B > 0, ta có
– Với các biểu thức A, B, C mà và , ta có
– Với các biểu thức A, B, C mà và , ta có
Trong bài viết này xin giới thiệu TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN. TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN giúp các em ôn luyện và thi môn Toán đạt kết quả cao, đồng thời đề thi cũng là tài liệu tốt giúp các thầy cô tham khảo trong quá trình dạy TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN.
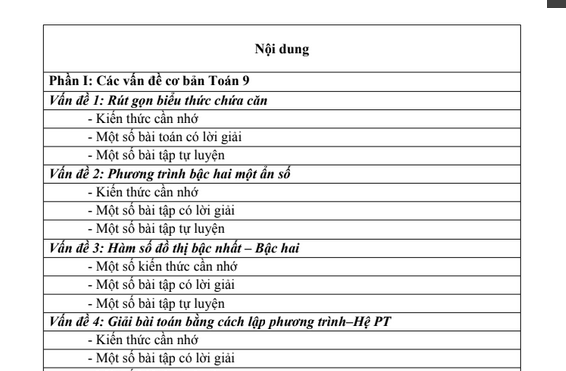
Tóm tắt nội dung TÀI LIỆU ÔN THI VÀO 10 MÔN TOÁN
| Nội dung |
| Phần I: Các vấn đề cơ bản Toán 9 |
| Vấn đề 1: Rút gọn biểu thức chứa căn |
| – Kiến thức cần nhớ |
| – Một số bài toán có lời giải |
| – Một số bài tập tự luyện |
| Vấn đề 2: Phương trình bậc hai một ẩn số |
| – Kiến thức cần nhớ |
| – Một số bài tập có lời giải |
| – Một số bài tập tự luyện |
| Vấn đề 3: Hàm số đồ thị bậc nhất – Bậc hai |
| – Một số kiến thức cần nhớ |
| – Một số bài tập có lời giải |
| – Một số bài tập tự luyện |
| Vấn đề 4: Giải bài toán bằng cách lập phương trình–Hệ PT |
| – Kiến thức cần nhớ |
| – Một số bài tập có lời giải |
| – Một số bài tập tự luyện |
| Vấn đề 5: Hệ phương trình bậc nhất hai ẩn số |
| – Kiến thức cần nhớ |
| – Một số bài tập có lời giải |
| – Một số bài tập tự luyện |
| Vấn đề 6: Bất đẳng thức – Giá trị Min – Max của biểu thức |
| – Một số bài tập tiêu biểu có lời giải |
| Vấn đề 7: Hình học phẳng và không gian |
| – Kiến thức cần nhớ |
| – Một số bài tập có lời giải |
| Phần II : Một số đề thi tiêu biểu có đáp án và biểu điểm |
| Phần III: Một số đề thi tự luyện theo cấu trúc đề thường gặp |
| Mục lục |
PHẦN I: CÁC VẤN ĐỀ CƠ BẢN CỦA TOÁN 9
VẤN ĐỀ I: RÚT GỌN BIỂU THỨC CHỨA CĂN BẬC HAI
- Kiến thức cần nhớ:
- Kiến thức cơ bản
- Căn bậc hai
- Căn bậc hai số học
- Với số dương a, số được gọi là căn bậc hai số học của a
- Số 0 cũng được gọi là căn bậc hai số học của 0
- Một cách tổng quát:
- So sánh các căn bậc hai số học
– Với hai số a và b không âm ta có:
- Căn thức bậc hai và hằng đẳng thức
- Căn thức bậc hai
- Với A là một biểu thức đại số , người ta gọi là căn thức bậc hai của A, A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn
- xác định (hay có nghĩa) A 0
- Hằng đẳng thức
- Với mọi A ta có
- Như vậy: + nếu A 0
+ nếu A < 0
- Liên hệ giữa phép nhân và phép khai phương
- Định lí: + Với A 0 và B 0 ta có:
+ Đặc biệt với A 0 ta có
- Quy tắc khai phương một tích: Muốn khai phương một tích của các thừa số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả với nhau
- Quy tắc nhân các căn bậc hai: Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới dấu căn với nhau rồi khai phương kết quả đó
- Liên hệ giữa phép chia và phép khai phương
- Định lí: Với mọi A 0 và B > 0 ta có:
- Quy tắc khai phương một thương: Muốn khai phương một thương a/b, trong đó a không âm và b dương ta có thể lần lượt khai phương hai số a và b rồi lấy kết quả thứ nhất chí cho kết quả thứ hai.
- Quy tắc chia các căn bậc hai: Muốn chia căn bậc hai của số a không âm cho số b dương ta có thể chia số a cho số b rồi khai phương kết quả đó.
- Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Đưa thừa số ra ngoài dấu căn
- Với hai biểu thức A, B mà B 0, ta có , tức là
+ Nếu A 0 và B 0 thì
+ Nếu A < 0 và B 0 thì
- Đưa thừa số vào trong dấu căn
+ Nếu A 0 và B 0 thì
+ Nếu A < 0 và B 0 thì
- Khử mẫu của biểu thức lấy căn
– Với các biểu thức A, B mà A.B 0 và B 0, ta có
- Trục căn thức ở mẫu
– Với các biểu thức A, B mà B > 0, ta có
– Với các biểu thức A, B, C mà và , ta có
– Với các biểu thức A, B, C mà và , ta có
- Căn bậc ba
- Khái niệm căn bậc ba:
- Căn bậc ba của một số a là số x sao cho x3 = a
- Với mọi a thì
- Tính chất
- Với a < b thì
- Với mọi a, b thì
- Với mọi a và thì
- Kiến thức bổ xung (*) Dành cho học sinh khá giỏi, học sinh ôn thi chuyên
- Căn bậc n
- Căn bậc n () của số a là một số mà lũy thừa n bằng a
- Căn bậc lẻ (n = 2k + 1)
- Mọi số đều có một và chỉ một căn bậc lẻ
- Căn bậc lẻ của số dương là số dương
- Căn bậc lẻ của số âm là số âm
- Căn bậc lẻ của số 0 là số 0
- Căn bậc chẵn (n = 2k )
- Số âm không có căn bậc chẵn
- Căn bậc chẵn của số 0 là số 0
- Số dương có hai căn bậc chẵn là hai số đối nhau kí hiệu là và




