- Tham gia
- 28/1/21
- Bài viết
- 86,007
- Điểm
- 113
tác giả
CHUYÊN ĐỀ CHIA HẾT TOÁN 8: CHUYÊN ĐỀ VỀ SỰ CHIA HẾT CỦA SỐ NGUYÊN
- Nếu a chia hết cho cả m và n, trong đó m, n là hai số nguyên tố cùng nhau thì a chia hết cho m.n
- Nếu tích a.b chia hết cho c, trong đó (b; c) = 1 thì a chia hết cho c
- Với p là số nguyên tố. Nếu a.b chia hết cho p thì hoặc a chia hết cho p hoặc b chia hết cho p
- Khi chia n + 1 số nguyên dương liên tiếp cho n luôn nhận được hai số dư bằng nhau
- Trong n số nguyên liên tiếp, luôn có duy nhất 1 số chia hết cho n
- Nếu thì tồn tại hai số nguyên x, y sao cho:
- Ta có:
- Ta có: với n là số tự nhiên lẻ
Phương pháp :
Bài 1: Chứng minh rằng với mọi số nguyên dương ta đều có: .
HD:
Ta có: , như vậy ta cần chứng minh .
Do là tích của 3 số nguyên liên tiếp nên chia hết cho cả 2 và 3
Bài 2: Chứng minh rằng :
HD :
Ta có:
Vì là ba số nguyên liên tiếp và
Bài 3: Chứng minh rằng:
HD:
Ta có:
Bài 4: Chứng minh rằng: lẻ
HD:
Vì m là số lẻ, Đặt
Khi đó ta có :
Thay vào A ta được :
Vì là tích ba số tự nhiên liên tiếp nên 6 Vậy
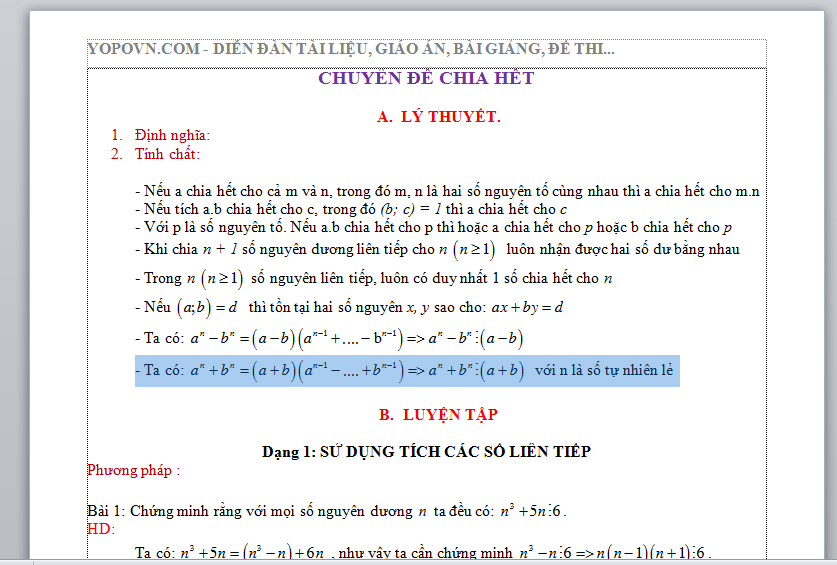
CHUYÊN ĐỀ CHIA HẾT
- LÝ THUYẾT.
- Định nghĩa:
- Tính chất:
- Nếu a chia hết cho cả m và n, trong đó m, n là hai số nguyên tố cùng nhau thì a chia hết cho m.n
- Nếu tích a.b chia hết cho c, trong đó (b; c) = 1 thì a chia hết cho c
- Với p là số nguyên tố. Nếu a.b chia hết cho p thì hoặc a chia hết cho p hoặc b chia hết cho p
- Khi chia n + 1 số nguyên dương liên tiếp cho n luôn nhận được hai số dư bằng nhau
- Trong n số nguyên liên tiếp, luôn có duy nhất 1 số chia hết cho n
- Nếu thì tồn tại hai số nguyên x, y sao cho:
- Ta có:
- Ta có: với n là số tự nhiên lẻ
- LUYỆN TẬP
Dạng 1: SỬ DỤNG TÍCH CÁC SỐ LIÊN TIẾP
Phương pháp :
Bài 1: Chứng minh rằng với mọi số nguyên dương ta đều có: .
HD:
Ta có: , như vậy ta cần chứng minh .
Do là tích của 3 số nguyên liên tiếp nên chia hết cho cả 2 và 3
Bài 2: Chứng minh rằng :
HD :
Ta có:
Vì là ba số nguyên liên tiếp và
Bài 3: Chứng minh rằng:
HD:
Ta có:
Bài 4: Chứng minh rằng: lẻ
HD:
Vì m là số lẻ, Đặt
Khi đó ta có :
Thay vào A ta được :
Vì là tích ba số tự nhiên liên tiếp nên 6 Vậy




