- Tham gia
- 28/1/21
- Bài viết
- 86,010
- Điểm
- 113
tác giả
Chuyên đề tích phân hàm ẩn LIST bài tập trắc nghiệm tích phân hàm ẩn NÂNG CAO LỚP 12
YOPOVN xin gửi đến quý thầy cô, các em học sinh Chuyên đề tích phân hàm ẩn LIST bài tập trắc nghiệm tích phân hàm ẩn NÂNG CAO LỚP 12. Đây là bộ Phương pháp giải hàm ẩn,Tích phân hàm ẩn -- Hoàng Phi Hùng,Nguyên hàm liên quan đến hàm ẩn,,Nguyên hàm từng phần hàm ẩn,Chuyên De nguyên hàm,Nguyên hàm hàm ẩn Đặng Việt Đông,Nguyên hàm từng phần dạng hàm ẩn,Nguyên hàm toanmath,... các bài tập trắc nghiệm tích phân hàm ẩn được soạn bằng file word. Thầy cô download file Chuyên đề tích phân hàm ẩn LIST bài tập trắc nghiệm tích phân hàm ẩn NÂNG CAO LỚP 12 tại mục đính kèm.
KIẾN THỨC CẦN NHỚ:
1. Các tính chất tích phân:
w với .
w
w
w
w
w
w
2. Công thức đổi biến số:
.
Phương pháp đổi biến số thường được sử dụng theo hai cách sau đây:
¨ Giả sử cần tính . Nếu ta viết được dưới dạng thì . Vậy bài toán quy về tính , trong nhiều trường hợp thì tích phân mới này đơn giản hơn .
¨ Giả sử cần tính . Đặt thỏa mãn thì
, trong đó
A. . B. . C. . D. .
1. DẠNG TOÁN: Đây là dạng toán tìm giá trị của tích phân của hàm số.
2. HƯỚNG GIẢI:
B1: Dựa vào biểu thức bên trong dấu tích phân, ta sử dụng phương pháp đổi biến số để xử lý bài toán.
B2: Sử dụng tính chất .
B3: Lựa chọn hàm thích hợp để tính giá trị tích phân.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Chọn B
Xét
Đặt
Đổi cận: .
.
Ä Mức độ 3
Cho hàm số . Biết tích phân ( là phân số tối giản). Giá trị bằng
A. . B. . C. . D. .
Chọn C
Ta có: .
Vậy .
Cho hàm số . Tích phân bằng:
A. . B. . C. . D. .
Xét
Đặt
Đổi cận: .
.
Câu 3. Cho hàm số . Tích phân ( là phân số tối giản), khi đó bằng:
A. . B. . C. . D. .
Xét
Đặt
Đổi cận: .
.
Cho hàm số liên tục trên và , . Tính
A. . B. . C. . D. .
Chọn B
Đặt . Khi thì . Khi thì .
Nên
.
Xét . Đặt .
Khi thì . Khi thì .
Nên .
Ta có .
Nên .
Cho là một nguyên hàm của hàm số trên tập và thỏa mãn . Tính tổng .
A. . B. . C. . D. .
Chọn C
Bảng khử dấu giá trị tuyệt đối:
Ta có: mà nên .
Ø mà nên .
Ø mà nên .
Ø mà nên .
Vậy .
Biết với . Tính .
A. . B. . C. . D. .
Chọn D
Ta có .
Do đó .
.
.
Cho hàm số có đạo hàm liên tục trên thỏa mãn , với mọi .Tích phân bằng
A. . B. . C. . D. .
Chọn C
Từ giả thiết ta có nên suy ra , .
Suy ra .
Đặt .
Với
Do đó .
Vậy .
Cho hàm số xác định và liên tục trên thoả Tích phân bằng
A. . B. . C. . D. .
Chọn B
Đặt .
Đổi cận:
Khi đó .
Cho hàm số xác định và liên tục trên thỏa mãn với . Tính .
A. . B. . C. . D.
Chọn B
Đặt và
Vậy .
Cho hàm số xác định thỏa và Giá trị của biểu thức bằng
A. B. C. D.
Chọn C
Ta có
và .
Do đó
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Chọn C
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Chọn B
Đặt . Đổi cận .
Do
.
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. 12. D. .
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
Xét
Đặt
Với
Ä Mức độ 4
Giá trị của tích phân bằng
A. . B. . C. . D. . 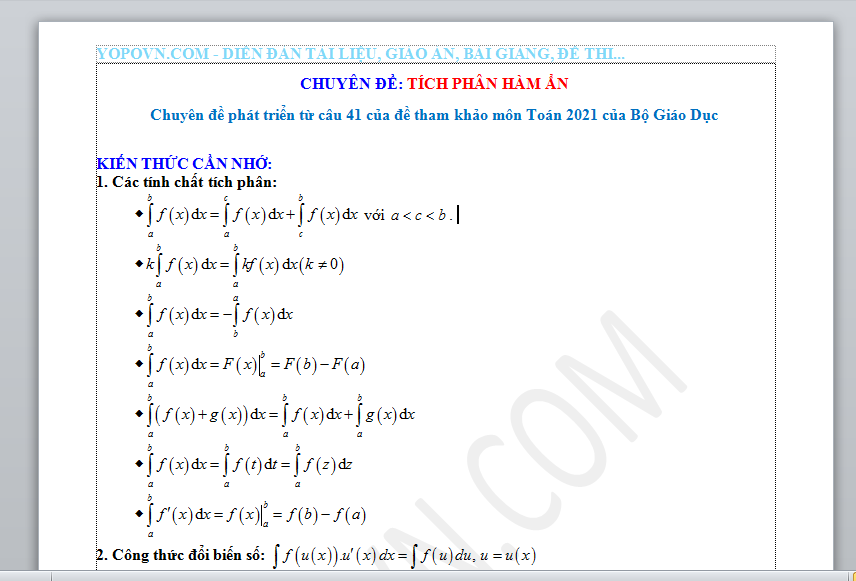
XEM THÊM:
YOPOVN xin gửi đến quý thầy cô, các em học sinh Chuyên đề tích phân hàm ẩn LIST bài tập trắc nghiệm tích phân hàm ẩn NÂNG CAO LỚP 12. Đây là bộ Phương pháp giải hàm ẩn,Tích phân hàm ẩn -- Hoàng Phi Hùng,Nguyên hàm liên quan đến hàm ẩn,,Nguyên hàm từng phần hàm ẩn,Chuyên De nguyên hàm,Nguyên hàm hàm ẩn Đặng Việt Đông,Nguyên hàm từng phần dạng hàm ẩn,Nguyên hàm toanmath,... các bài tập trắc nghiệm tích phân hàm ẩn được soạn bằng file word. Thầy cô download file Chuyên đề tích phân hàm ẩn LIST bài tập trắc nghiệm tích phân hàm ẩn NÂNG CAO LỚP 12 tại mục đính kèm.
CHUYÊN ĐỀ: TÍCH PHÂN HÀM ẨN
Chuyên đề phát triển từ câu 41 của đề tham khảo môn Toán 2021 của Bộ Giáo Dục
Chuyên đề phát triển từ câu 41 của đề tham khảo môn Toán 2021 của Bộ Giáo Dục
KIẾN THỨC CẦN NHỚ:
1. Các tính chất tích phân:
w với .
w
w
w
w
w
w
2. Công thức đổi biến số:
.
Phương pháp đổi biến số thường được sử dụng theo hai cách sau đây:
¨ Giả sử cần tính . Nếu ta viết được dưới dạng thì . Vậy bài toán quy về tính , trong nhiều trường hợp thì tích phân mới này đơn giản hơn .
¨ Giả sử cần tính . Đặt thỏa mãn thì
, trong đó
- BÀI TẬP MẪU
A. . B. . C. . D. .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm giá trị của tích phân của hàm số.
2. HƯỚNG GIẢI:
B1: Dựa vào biểu thức bên trong dấu tích phân, ta sử dụng phương pháp đổi biến số để xử lý bài toán.
B2: Sử dụng tính chất .
B3: Lựa chọn hàm thích hợp để tính giá trị tích phân.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn B
Xét
Đặt
Đổi cận: .
.
Bài tập tương tự và phát triển:
Ä Mức độ 3
Cho hàm số . Biết tích phân ( là phân số tối giản). Giá trị bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có: .
Vậy .
Cho hàm số . Tích phân bằng:
A. . B. . C. . D. .
- Lời giải
Xét
Đặt
Đổi cận: .
.
Câu 3. Cho hàm số . Tích phân ( là phân số tối giản), khi đó bằng:
A. . B. . C. . D. .
- Lời giải
Xét
Đặt
Đổi cận: .
.
Cho hàm số liên tục trên và , . Tính
A. . B. . C. . D. .
Lời giải
Chọn B
Đặt . Khi thì . Khi thì .
Nên
.
Xét . Đặt .
Khi thì . Khi thì .
Nên .
Ta có .
Nên .
Cho là một nguyên hàm của hàm số trên tập và thỏa mãn . Tính tổng .
A. . B. . C. . D. .
Lời giải:
Chọn C
Bảng khử dấu giá trị tuyệt đối:
Ta có: mà nên .
Ø mà nên .
Ø mà nên .
Ø mà nên .
Vậy .
Biết với . Tính .
A. . B. . C. . D. .
Lời giải:
Chọn D
Ta có .
Do đó .
.
.
Cho hàm số có đạo hàm liên tục trên thỏa mãn , với mọi .Tích phân bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Từ giả thiết ta có nên suy ra , .
Suy ra .
Đặt .
Với
Do đó .
Vậy .
Cho hàm số xác định và liên tục trên thoả Tích phân bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Đặt .
Đổi cận:
Khi đó .
Cho hàm số xác định và liên tục trên thỏa mãn với . Tính .
A. . B. . C. . D.
Lời giải
Chọn B
Đặt và
Vậy .
Cho hàm số xác định thỏa và Giá trị của biểu thức bằng
A. B. C. D.
Lời giải
Chọn C
Ta có
và .
Do đó
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Lời giải:
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Lời giải:
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Lời giải:
Chọn A
Đặt . Đổi cận .
Do
.
Cho hàm số . Khi đó bằng
A. . B. . C. . D. .
Lời giải:
Chọn B
Đặt . Đổi cận .
Do
.
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
- Lời giải:
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. 12. D. .
- Lời giải:
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
- Lời giải:
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
- Lời giải:
Xét
Đặt
Với
Cho hàm số . Tính tích phân .
A. . B. . C. . D. .
- Lời giải:
Xét
Đặt
Với
Ä Mức độ 4
Giá trị của tích phân bằng
A. . B. . C. . D. .
XEM THÊM:
- Các dạng bài tập nguyên hàm tích phân
- Tài liệu ôn thi thpt quốc gia 2022 môn toán
- Bài tập trắc nghiệm ứng dụng của tích phân trong hình học
- Tư duy logic tìm tòi lời giải hệ phương trình
- Chuyên đề giá trị lớn nhất giá trị nhỏ nhất của hàm số
- Bộ Đề thi Khảo sát chất lượng Toán lớp 12 Giữa kì 2
- Hình học giải tích oxy
- Đề ôn tập học kì 2 lớp 12 môn toán
- ỨNG DỤNG TÍCH PHÂN LỚP 12
- KỸ THUẬT GIẢI TOÁN TÍCH PHÂN
- chuyên đề ôn thi thpt quốc gia môn TOÁN
- Mũ logarit trong đề thi thpt quốc gia
- Chuyên đề nguyên hàm tích phân và ứng dụng
- Hàm số và các ứng dụng của đạo hàm
- Các chủ đề hình học giải tích trong không gian
- Các dạng bài tập số phức thi thpt quốc gia
- BỒI DƯỠNG HỌC SINH GIỎI HÌNH HỌC KHÔNG GIAN
- Ôn tập toán lớp 12 học kì 1
- Các câu hỏi trắc nghiệm thể tích khối đa diện
- Xác định hệ số của hàm bậc 3
- Tài liệu xét chiều biến thiên của hàm số lớp 12
- Các dạng toán tích phân thường gặp
- Bài Tập Trắc Nghiệm Hình Học 12 CẢ NĂM
- Phương pháp tìm tiệm cận đứng bằng casio
- Tìm tiệm cận ngang của hàm số bằng máy tính
- Đề thi học kì 2 môn toán 12
- Bài tập trắc nghiệm về số phức có đáp án
- Chuyên đề số phức ôn thi thpt quốc gia
- Chuyên đề dãy số bồi dưỡng học sinh giỏi
- Đề Thi Chọn HSG Toán Lớp 12
Đại số và giải tích 12 nâng cao - câu hỏi trắc nghiệm về toán học
- ÔN TẬP TOÁN GIỮA KÌ 2 LỚP 12
- Đề Thi HSG Toán 12 Có Đáp Án
- Trắc nghiệm toán lớp 12 có đáp án
- Bài tập trắc nghiệm thể tích khối chóp
- câu hỏi trắc nghiệm toán lớp 12
- Đề Thi HSG Toán 12 NĂM 2021
- Trắc nghiệm phương pháp tọa độ trong không gian
- Đề kiểm tra phương pháp tọa độ trong không gian
- Đề thi giữa học kì 2 lớp 12 môn toán
- Đề khảo sát chất lượng toán 12
- Đề thi học kì 2 môn toán 12 trắc nghiệm
- Đề thi giữa kì 2 môn toán lớp 12 violet
- Đề cương ôn tập toán 12 học kì 2
- Ôn tập chuyên đề nguyên hàm tích phân
- Ôn toán lớp 12 cấp tốc




